Welcome to the fourth installment of The World Through Sound. In previous articles we discussed properties of sound, including sound speed, and wavelength. Today, we are going to take a step back and consider sound on a more fundamental level. We are going to discuss the concept of “equilibrium,” and how it relates to the world around us in surprising ways. Finally we will tie equilibrium to sound through “acoustic pressure,” to show that all sound is actually just variation around equilibrium.
Equilibrium is all around us. Almost everything is either in equilibrium or moving towards it. To illustrate equilibrium, one of my acoustics professors once asked the class to look around the room and then close their eyes for a few moments. When we opened our eyes we expected to see some surprise that our teacher had unveiled. Instead we saw the same old classroom, completely unchanged. “Does everything look the same?” He said, a satisfied grin creeping across his face. “That’s because it’s all at equilibrium!”
So what is equilibrium? Equilibrium occurs when all forces acting on a system are in balance. When this is the case, the system does not change until some outside action moves the system out of equilibrium. Any object that is at rest is at equilibrium. For example, an object sitting flat on a table has the force of gravity acting on it to pull it down, while an equal force acts on it from the table. Because these forces are in balance the object does not fall or fly away, and it will continue to sit in this way until some additional force is added, like a person picking up the object.
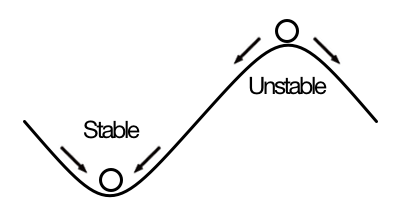
When just outside of equilibrium, forces move systems towards stable equilibrium, but away from unstable equilibrium.
Equilibrium comes in two broad forms: stable and unstable. Stable equilibrium means that if the system is moved slightly away from equilibrium, it will move back to the same equilibrium point. A system in unstable equilibrium, on the other hand, will tend to move away from that point. An example of stable equilibrium, is a ball sitting at the bottom of a valley. If you move the ball up the hill on either side, gravity will cause the ball to roll back down to the lowest point. A ball sitting at the top of a hill, on the other hand, is unstable, because if it rolls to either side, it will not stop until it reaches the bottom of the hill (a different equilibrium point than it started at).
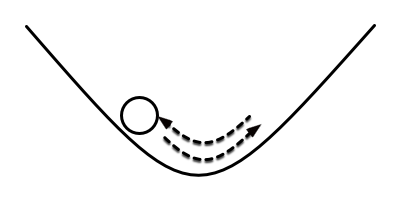
Acoustics is mostly concerned with behavior around stable equilibrium, so let’s look deeper into the ball sitting at the bottom of a valley. If the ball is moved up the hill to the left and released, it will begin to roll down the hill towards the center. Once it reaches that point, however, it will continue to roll because of momentum, overshooting and rolling up the hill to the right. Once it has gotten high enough, its direction of motion will change, and it will move back towards the center again. Assuming that the ball has not lost too much energy to friction, this process will continue, oscillating back and forth. And if we plot out the location of the ball over time, relative to that center point, a familiar picture will emerge: a sinusoid. You can see this in action at home using a round bottomed bowl and a small marble.
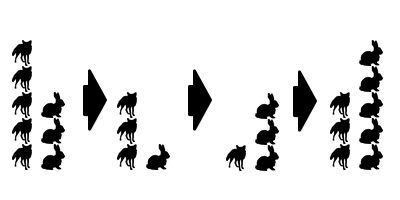
Predator and prey populations vary around equilibrium, with the predator population lagging behind that of the prey.
Equilibrium applies to more than just physics. Anything that has a natural balance point might reach equilibrium, and variations around equilibrium will behave in similar manners even with wildly different systems. A fun example of this is the populations of predator and prey animals in the wild, which follow what are known as the Lotka-Volterra Equations. In these equations we have two populations: predators and prey (foxes and rabbits, for example). While the prey feed off the land, the predators feed off of the prey. When there is a lot of prey, the predator population will increase, because they have a lot of food. When there are a lot of predators, then the prey population will decrease because they are getting eaten. Ultimately, the Lotka-Volterra Equations lead to some form of equilibrium, some population of predator and prey where the predators eat the prey only as fast as the prey can reproduce. Using this equilibrium point, you can predict if either group is in “overpopulation” or “underpopulation,” and how that group will trend in the future. If there are more predators than equilibrium would allow, for example, you can expect that population to decrease, while fewer predators would suggest a future increase in the predator population.
When the populations deviate from equilibrium they can oscillate, much like the ball rolling back-and-forth in the valley. Overpopulation of predators will decrease the population of its prey, causing a food shortage that leads to a decrease in the predator population. When the predator population is reduced, this leaves room for more prey to breed, but this does not simply happen overnight, and the predator population will continue to decrease even as the prey is beginning their comeback. Ultimately, the predators will become underpopulated, opening the possibility for the prey animals to overpopulate. Following this chain of logic, it should become apparent that the populations are moving back and forth over time, with the population of the predators trailing behind that of the prey they eat. In any given environment, there are many interactions like this happening all the time, forming a delicate ecological balance, which is always at risk of outside forces like extreme weather or the actions of humans.
Populations are just one example of this phenomena. Nearly any simple system that has a point of stable equilibrium will have such oscillations, from pendulums to ocean waves to playground swings. Keep an eye out for these, and perhaps you will find that things you thought were very different behave in much the same ways.
So what does this have to do with acoustic pressure? Simply put, we are constantly surrounded by a system in equilibrium: the air. While the tiny particles of the air itself are in a state of constant motion, the pressure of air (the force air exerts on the world around it) is relatively stable, with an ambient pressure determined largely by altitude and the weather. Acoustic pressure (essentially a fancy phrase for “sound”) is the tiny variation that occurs around that ambient pressure, or to put it another way, the oscillation around equilibrium (to see what “tiny variation” means to a scientist, refer to the previous article on wavelength).
Not only is the air itself oscillating around equilibrium, so too are the sources of sound around us. When you knock on a wooden table, the sound is generated because the table is in a state of equilibrium until the knock causes it to move. As the table returns to equilibrium, it vibrates back and forth briefly, generating sound by pushing on the air around it. A loud speaker is also in a state of equilibrium, until the electrical signals used to control it cause it move out of that position. Even the way we listen involves oscillation around equilibrium, with our eardrums and the tiny mechanisms of the middle and inner ear moving back-and-forth in response to sound.
Ultimately, equilibrium is one of those concepts that reaches over many areas of science, from physics to biology. Without equilibrium, acoustics could hardly exist, as sound is so closely tied to those tiny variations that occur when systems move away from equilibrium. The next time you hear a sound, think to yourself “What is the change around equilibrium that I just heard?” Because, in the end, that is exactly what you are hearing, the motions of a world near equilibrium.
In the next installment of The World Through Sound, we will talk about the most popular unit for measuring the strength of a sound: Decibels. A scale uniquely designed to handle values that range from the very small to the very large, and that happens to map well to the sense of loudness that humans naturally perceive.
Andrew “Pi” Pyzdek is a PhD candidate in the Penn State Graduate Program in Acoustics. Andrew’s research interests include array signal processing and underwater acoustics, with a focus on sparse sensor arrays and the coprime array geometry. Andrew also volunteers his time doing acoustics outreach and education as a panelist and moderator on the popular AskScience subreddit and by curating interesting acoustics news for a general audience at ListenToThisNoise.com.
Contact info: andrew@pyzdek.com