Welcome to the third installment of “The World Through Sound,” the Acoustics Today web series that shows how understanding just a few concepts in acoustics can change the way you see the world around you. Last time we considered frequency and how the relationship between frequency and time for acoustic waves can help dispel the mystery of the Uncertainty Principle of quantum mechanics. In this article, we will combine the concepts of the last two articles on sound speed and frequency to talk about wavelength, and the importance of scale when dealing with physics.
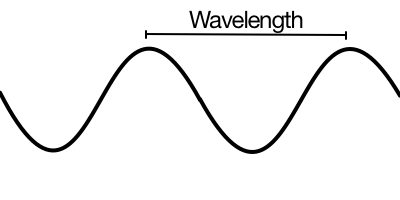
Wavelength is the size of a wave, measured from peak to peak.
Wavelength is one of the more straightforward acoustics concepts to imagine. It is simply the size of a wave, measured from one peak to the next. If one imagines a sound wave as something like a water wave, then the wavelength is simply the distance from the crest of one wave to the next nearest crest. Thus, if the distance between two peaks is 1 m, then the wavelength is 1 m. There is a direct relation between wavelength, frequency, and sound speed. Namely, if we know the frequency (which is the number of wave repetitions per second, often given in Hertz, or Hz) and the sound speed (which is the speed the wave travels in meters per sec), then we can find the wavelength using the equation wavelength=speed/frequency.
Put another way, wavelength is the distance that a wave travels before the next wave starts. That means that at a given sound speed, as frequency gets higher, the time between repetitions decreases and the wavelength gets shorter, and vice versa.

Waves can bend around small objects with ease, while larger objects may block those waves.
Wavelength is the essential quantity to know when trying to understand how waves move through the world. Long wavelengths bend around objects that are smaller then themselves, while short wavelengths reflect off of or are absorbed by those same objects. Thus, a sound with a wavelength of 34 cm in air (1,000 Hz) will not be hampered by an object that is less than 34 cm in diameter, but a larger object may interfere with or entirely block that wave.
Often people talk about “long” and “short,” but what is really meant by these terms?” How does one draw the line between those admittedly fuzzy and highly subjective categories? To answer this question, we must understand the concept of scale. Scale is important throughout science, from biology to physics, though not all disciplines give it formal treatment.

Scale is relative. A pebble that may seem huge compared to an ant would be tiny next to an elephant!
To see how a physicist thinks of scale, think about this question: “How big is a 1-inch (2.54 cm) rock?” If your answer is “not very big,” then you are thinking like a human. But imagine for a second that you were an ant. That rock would seem like a hill! If you were a mouse, the rock would be like a small boulder. If you are a human, the rock is merely a pebble. And if you were an elephant, the rock is like a tiny piece of gravel. Scale applies to more than just physical size, though. For example, you might have heard of a “geologic time scale,” which refers to periods of time that are long enough to observe significant changes in the Earth itself. Almost every quantity can cover a wide scale, be that distance, pressure, time, or even money.
When talking about differences of scale, the term used most often is “order of magnitude,” which is another way of saying power of ten. If one were to say something was “an order of magnitude larger,” what they are really saying is that it is ten times larger than whatever it is being compared to. If something is two orders of magnitude larger, that would be 100 times the size. The order of magnitude is so important that it is part of scientific notation. For example, 5,000,000,000 meters (m) might be written as 5.0×109 m, with the 9 in the exponent being the order of magnitude. A famous video commissioned by IBM runs through the scales of the universe in orders of magnitude, from the largest to the smallest.
While there are certainly exceptions, two quantities are considered comparable when they are within one order of magnitude of each other. Beyond that, we describe one as being “much larger” or “much smaller” than the other. While this may seem like just a semantic difference, in many physics equations having one quantity much smaller or much larger causes the math to clean up to much simpler forms, which corresponds to much simpler physical behavior.
While scale is important throughout science, there are few places where it is more apparent than with wavelength and sound. Wavelength of audible sounds, as it turns out, covers a very large range of scales. On the large end, you have low frequency waves with wavelengths of up to 17 meters (20 Hz), while the highest frequencies can be as small as 1.7 centimeters (20,000 Hz). Compare this to the wavelengths of visible light (430-790 nanometers), and not only do you find that sound covers a much wider range of scales (four orders of magnitude), but it also covers a range that is squarely at the scale of human experience.
For an example of how wavelength determines the behavior or sound, consider living in an apartment with a noisy next door neighbor. If that neighbor turns up their stereo, you might hear the bass clearly through the wall. The bass notes are low frequency, with very long wavelengths. Wavelengths so long, in fact, that the plaster drywall separating you from the music would be considered “very thin.” The higher notes, on the other hand, get handily blocked by the wall, resulting in the “muffled” sound that is often associated with blocked sources.
Wavelength also determines how easy it is to find the direction of a sound. You may have heard, for example, that the placement of a subwoofer in a room does not make a big difference for a sound system. As it is often described, “low frequencies” are not directional. What this really means is that the wavelengths of low frequencies (which can be more than a meter long) are so large that the listener’s head is much smaller than a wavelength. As a result, there is very little difference between the sound received by the left and right ears, and the difference of the received sound at the two ears is what the brain uses to calculate the direction of a sound.
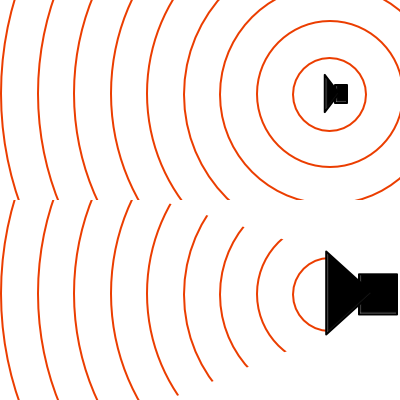
Size matters when designing loudspeakers. Small speakers put out sound in all directions, while large speakers broadcast in a cone in front of them.
Even the way that sound is generated is affected by wavelength. For loudspeakers that are much smaller than a wavelength, sound will tend to spread evenly in all directions. This is called “omni-directionality.” When loudspeakers get larger, they become more directional, with speakers that are very large compared to a wavelength projecting in a cone-like shape in front of themselves. This is a large part of why high-end speaker systems are made up of multiple loudspeakers (called drivers). The size of each driver is chosen for the wavelengths of sound it reproduces best, ensuring that the sound system can cover the whole range from 17 meters to 1.7 centimeters.
Of course, while the wavelength for audible sounds is relatively wide, it is still limited. For sounds beyond the audible frequencies, however, wavelengths can be even more extreme. Ultrasound (sounds above the limit of human hearing at ~20 kHz), has wavelengths so small that their reflections can be used to image the tiny structures inside our bodies or used by bats and dolphins to detect and differentiate between prey objects. Infrasound (generally defined as frequencies below the lower limit of human hearing or 20 Hz), on the other hand, can have wavelengths so long that the sounds need to be measured using massive networks of sensors working in unison

Infrasound wavelengths can be so long that huge setups are needed to measure them. Photo credit: CTBTO.
The range of scales, from the size of the observable universe to the width of a single neutron is about 40 orders of magnitude (see video above). While the range of wavelengths for sound is not nearly so large, the range that it covers is important for humans, and is a range that we experience in our daily lives. As a result, by listening carefully, we can hear how both the “very large” and the “very small” alter the ways sounds move through the world around us. We can hear how a thick pillow absorbs all but the deepest of sounds, while a tiny speaker can only reproduce the highest.
Expect to see wavelength come up again and again throughout this series. It is a fundamental concept with far-reaching implications for everything from what allows a medium to support sound, to what makes an acoustic resonator ring. And the next time you see the term, keep an eye out for phrases like “order of magnitude,” “much larger,” and “much smaller,” because when it comes to wavelength, scale is everything.
Andrew “Pi” Pyzdek is a PhD candidate in the Penn State Graduate Program in Acoustics. Andrew’s research interests include array signal processing and underwater acoustics, with a focus on sparse sensor arrays and the coprime array geometry. Andrew also volunteers his time doing acoustics outreach and education as a panelist and moderator on the popular AskScience subreddit and by curating interesting acoustics news for a general audience at ListenToThisNoise.com.
Contact info: andrew@pyzdek.com

