Page 56 - Fall2019

Nonlinear Acoustics Today
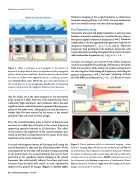
Figure 1. When a nonlinear wave propagates in the absence of dispersion, its shape distorts due to the dependence of the propagation speed on the local wave amplitude. This phenomenon is observed both for waves in shallow water (top row) and for a nonlinear acoustic wave (bottom three rows). Third row: gray scale representation of the sound pressure in the second row; fourth row: corresponding frequency (f) spectrum (S) at different distances from the source.
that the echoes are at the same frequency as the transmitted pulse, around 2-5 MHz. However, if the emitted pulses have sufficiently high amplitude, then nonlinear effects become significant and a second harmonic is generated during propa- gation of the probe wave. Although the second harmonic is weaker than the wave emitted by the source, it has several properties that can result in better images.
First, the second harmonic pulse is shorter in duration and narrower in width than the pulse at the source frequency, improving spatial resolution in all directions. This effect occurs because the amplitude of the second harmonic gen- erated in the body is proportional to the square of the local amplitude at the source frequency.
A second advantageous feature of the image built using the second harmonic is that near the ultrasound probe, where heterogeneities in the body wall introduce strong scattering of the probe beam, the second harmonic has not yet been generated to any significant degree. Imaging at the second harmonic thus substantially reduces the echoes and rever- beration from the body wall, which, in turn, significantly improves the quality of images (Figure 2, bottom right).
Nonlinear imaging at the second harmonic is called tissue harmonic imaging (Burns et al., 2000). It is now standard on most ultrasound systems used for echocardiography.
The Parametric Array
Generation of second and higher harmonics is only one mani- festation of acoustic nonlinearity. Consider the case where a bifrequency signal is radiated at frequencies f1 and f2. Quadratic nonlinearity in the first approximation generates sound in the medium at frequencies |f1 − f2|, f1 + f2, 2f1, and 2f2. These new frequencies then participate in the nonlinear interaction, with energy ultimately cascading throughout the spectrum to all pos- sible combination frequencies |mf1 ± nf2|, m, n = 1, 2, ...
A means of creating a very narrow beam of low-frequency sound is accomplished by radiating a bifrequency waveform from the transducer. If the initial two (primary) frequencies are close together, then among all frequencies, including the primary frequencies f1 and f2, the most “enduring” of them all is the difference frequency ( fD = | f2 − f1|). Because viscous
Figure 2. Use of nonlinear effects in ultrasound imaging — tissue harmonic imaging. Top: red indicates the fundamental and blue the second harmonic that originates in the patient’s body and is therefore less subject to deleterious effects of the body wall and provides better resolution due to its narrower beam. Middle: frequency spectrum of the ultrasound echo. Bottom: comparison of fundamental (linear; left) and harmonic (nonlinear; right) ultrasound images of the heart. Images courtesy of M. A. Averkiou.
56 | Acoustics Today | Fall 2019