Page 11 - Winter 2008

Fig. 7. 2-D spatial distribution and 1-D cross-section view of an experimentally measured time reversed focus which is diffraction limited. Warmer colors corre- spond to larger amplitudes.
tive TR procedure was developed by Prada et al.
gressively increase the focusing of energy onto an individual, strong wave scatterer (the strongest in the medium under interrogation). The Iterative TRM (ITRM) works in a pulse- echo mode. A pulse is sent out and reflects from one or more scatterers. This reflection is detected by the ITRM and then time reversed and rebroadcast. This procedure is repeated and the focal amplitude on the scatterer(s) is thereby pro- gressively increased until the energy is clearly focusing on the strongest scatterer in the medium. ITRM is, in essence, an experimental summation procedure. The ITRM can only focus on the strongest scatterering signal present in the time window used, and thus weaker scatterering signals present in the same time window are not illuminated.
To identify multiple scatterers, Prada et al. developed a well-known procedure called the DORT method, from the
18,19
French acronym for Decomposition of the TR Operator. Consider a medium with several well-resolved point-like scatterers of varying strengths. The DORT method requires that for a given array of N transducers that, one by one, each transducer emits an impulse and the reflected signals from the scatterers are then detected by all of the transducers with- in the array. This set of signals can be arranged as a row of a matrix. There are exactly N rows. Distinct rows correspond to different source transducers. Each element of this matrix consists of a temporal signal. A corresponding matrix con- taining the Fourier transforms of the signals is then calculat- ed. A linear algebra technique called Singular Value Decomposition (SVD) can be used to extract, for each fre- quency, a set of N numbers, called singular values, character- izing the impulse response matrix. These numbers are like fin- gerprints of the set of scatterers. In fact, each of these num- bers is proportional to the square of the reflectivity of a spe- cific scatterer. More importantly, SVD associates each singu- lar value, i.e. a scatterer, to a set of N signals. This set is called the singular vector of the impulse response matrix relative to that singular value. Physically, it is the set of Fourier trans- forms of the signals to be applied to the array to focus on that specific scatterer. The DORT theory and method have been
16,17
to pro-
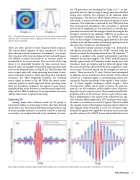
These are often narrow in their frequency-band response. The narrow-band response of these transducers is due to their inherent natural frequencies (resonances). As a result, they ring down after wave excitation at their natural frequen- cies (whether excited electrically as in transmit mode, or acoustically as in receive mode). The net result of the ring down is to temporally broaden the time reversed focus. Figure 8 shows an example of what influence ring down may have on the temporal focus. In Fig. 8a the TRM recreates the source signal quite well, when operating away from a trans- ducer resonance; however, when operating on a transducer resonance, the TRM temporally broadens the recreated source signal as shown in Fig. 8b. While the source recon- struction quality is much improved when operating away from the transducer resonance, the signal to noise ratio is diminished due to the decrease in sensitivity and output effi- ciency of the TRM transducers. In an experiment, one must address these issues to optimize focusing.
Exploiting TR
Among many other advances made by the group at Laboratoire Ondes et Acoustique in Paris, they have devised the means to use TR to locate individual strong scatterers and to locate multiple scatterers (a scatterer could be a sidewall, an interface, or an object located in the medium). An itera-
Fig. 8. Experimentally measured temporal signal representing a time reversed focus (in blue) and the source function it attempted to recreate (in red).
Time Reversal 9