Page 15 - Winter2014

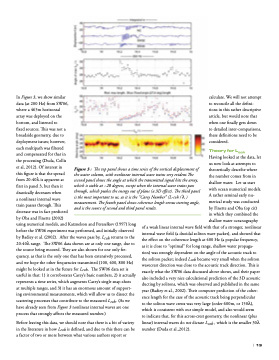
In Figure 3, we show similar data (at 200 Hz) from SW06, where a 465m horizontal array was deployed on the bottom, and listened to
fixed sources. This was not a broadside geometry, due to deployment issues; however, each multipath was filtered and compensated for that in the processing (Duda, Collis et al, 2012). Of interest in this figure is that the spread from 20-40λ is apparent at first in panel 3, but then it drastically decreases when
a nonlinear internal wave
train passes through. This
decrease was in fact predicted
by Oba and Finette (2002)
using numerical models, and Katznelson and Pereselkov (1997) long before the SW06 experiment was performed, and initially observed by Badiey et al. (2002). After the waves pass by, Lcoh returns to the 20-40λ range. The SW06 data shown are at only one range, due to the source being moored. They are also shown for one only fre- quency, as that is the only one that has been extensively processed, and we hope the other frequencies transmitted (100, 400, 800 Hz) might be looked at in the future for Lcoh. The SW06 data set is useful in that: 1) it corroborates Carey’s basic numbers, 2) it actually represents a time series, which augments Carey’s single snap-shots
at multiple ranges, and 3) it has an enormous amount of support- ing environmental measurements, which will allow us to dissect the scattering processes that contribute to the measured Lcoh. (As we have already seen from Figure 3 nonlinear internal waves are one process that strongly affects the measured number.)
Before leaving this data, we should note that there is a bit of variety in the literature in how Lcoh is defined, and due to this there can be a factor of two or more between what various authors report or
calculate. We will not attempt to reconcile all the defini- tions in this rather descriptive article, but would note that when one finally gets down
to detailed inter-comparisons, these definitions need to be considered.
Theory for Lcoh
Having looked at the data, let us now look at attempts to theoretically describe where the number comes from in shallow water. Let us start with ocean numerical models. A rather seminal early nu- merical study was conducted by Finette and Oba (op cit) in which they combined the shallow water oceanography
of a weak linear internal wave field with that of a stronger, nonlinear internal wave field (a dnoidal soliton wave packet), and showed that the effect on the coherence length at 400 Hz (a popular frequency, as it is close to “optimal” for long range, shallow water propaga- tion) was strongly dependent on the angle of the acoustic track to the soliton packet; indeed Lcoh became very small when the soliton wavecrest direction was close to the acoustic track direction. This is exactly what the SW06 data discussed above shows, and their paper also included a very nice calculational prediction of the 3D acoustic ducting by solitons, which was observed and published in the same year (Badiey et al., 2002). Their computer prediction of the coher- ence length for the case of the acoustic track being perpendicular
to the soliton wave crests was very large (order 600m, or 150λ), which is consistent with our simple model, and also would seem
to indicate that, for this across-crest geometry, the nonlinear (plus linear) internal waves do not dictate Lcoh , which is the smaller 30λ number (Duda et al.,2012).
Figure 3 : The top panel shows a time series of the vertical displacement of the water column, with nonlinear internal wave trains very evident.The second panel shows the angle at which the transmitted signal hits the array, which is stable at ~28 degrees, except when the internal wave trains pass through, which pushes the energy out of plane (a 3D effect). The third panel is the most important to us, as it is the “Carey Number” (L-coh / λ ) measurement. The fourth panel shows coherence length versus steering angle, and is the source of second and third panel results.
| 13