Page 51 - Summer2020

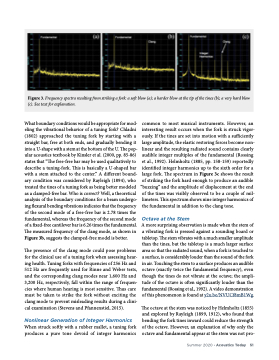
Figure 3. Frequency spectra resulting from striking a fork: a soft blow (a); a harder blow at the tip of the tines (b); a very hard blow (c). See text for explanation.
What boundary conditions would be appropriate for mod- eling the vibrational behavior of a tuning fork? Chladni (1802) approached the tuning fork by starting with a straight bar, free at both ends, and gradually bending it into a U-shape with a stem at the bottom of the U. The pop- ular acoustics textbook by Kinsler et al. (2000, pp. 85-86) states that “The free-free bar may be used qualitatively to describe a tuning-fork. This is basically a U-shaped bar with a stem attached to the center.” A different bound- ary condition was considered by Rayleigh (1894), who treated the tines of a tuning fork as being better modeled as a clamped-free bar. Who is correct? Well, a theoretical analysis of the boundary conditions for a beam undergo- ing flexural bending vibrations indicates that the frequency of the second mode of a free-free bar is 2.78 times the fundamental, whereas the frequency of the second mode of a fixed-free cantilever bar is 6.26 times the fundamental. The measured frequency of the clang mode, as shown in Figure 3b, suggests the clamped-free model is better.
The presence of the clang mode could pose problems for the clinical use of a tuning fork when assessing hear- ing health. Tuning forks with frequencies of 256 Hz and 512 Hz are frequently used for Rinne and Weber tests, and the corresponding clang modes near 1,600 Hz and 3,200 Hz, respectively, fall within the range of frequen- cies where human hearing is most sensitive. Thus care must be taken to strike the fork without exciting the clang mode to prevent misleading results during a clini- cal examination (Stevens and Pfannenstiel, 2015).
Nonlinear Generation of Integer Harmonics
When struck softly with a rubber mallet, a tuning fork produces a pure tone devoid of integer harmonics
common to most musical instruments. However, an interesting result occurs when the fork is struck vigor- ously. If the tines are set into motion with a sufficiently large amplitude, the elastic restoring forces become non- linear and the resulting radiated sound contains clearly audible integer multiples of the fundamental (Rossing et al., 1992). Helmholtz (1885, pp. 158-159) reportedly identified integer harmonics up to the sixth order for a large fork. The spectrum in Figure 3c shows the result of striking the fork hard enough to produce an audible
“buzzing” and the amplitude of displacement at the end of the tines was visibly observed to be a couple of mil- limeters. This spectrum shows nine integer harmonics of the fundamental in addition to the clang tone.
Octave at the Stem
A more surprising observation is made when the stem of a vibrating fork is pressed against a sounding board or tabletop. The stem vibrates with a much smaller amplitude than the tines, but the tabletop is a much larger surface area so that the radiated sound, when a fork is touched to a surface, is considerably louder than the sound of the fork in air. Touching the stem to a surface produces an audible octave (exactly twice the fundamental frequency), even though the tines do not vibrate at the octave; the ampli- tude of the octave is often significantly louder than the fundamental (Rossing et al., 1992). A video demonstration of this phenomenon is found at y2u.be/NVUCf8mB1Wg.
The octave at the stem was noticed by Helmholtz (1855) and explored by Rayleigh (1899, 1912), who found that bending the fork tines inward could reduce the strength of the octave. However, an explanation of why only the octave and fundamental appear at the stem was not pro-
Summer 2020 • Acoustics Today 51