Welcome to the fifth installment of The World Through Sound. Last time, we discussed the concepts of equilibrium and acoustic pressure, and how almost any variation around equilibrium can bear a striking resemblance to the behavior of sound. Today, we are going to look a little more at acoustic pressure, and one of the most valuable units for measuring sound: the decibel. We will also talk about how adopting a metric like the decibel can change the way we interact with the world.
The decibel was first invented by Bell Laboratories in the 1920’s. Originally used to measure power loss in telecommunication systems, this unit was valuable because it transformed the laborious task of multiplying losses from different portions of the system into a problem of simple addition. Since that time, the decibel has been adopted in many different fields, notably acoustics.
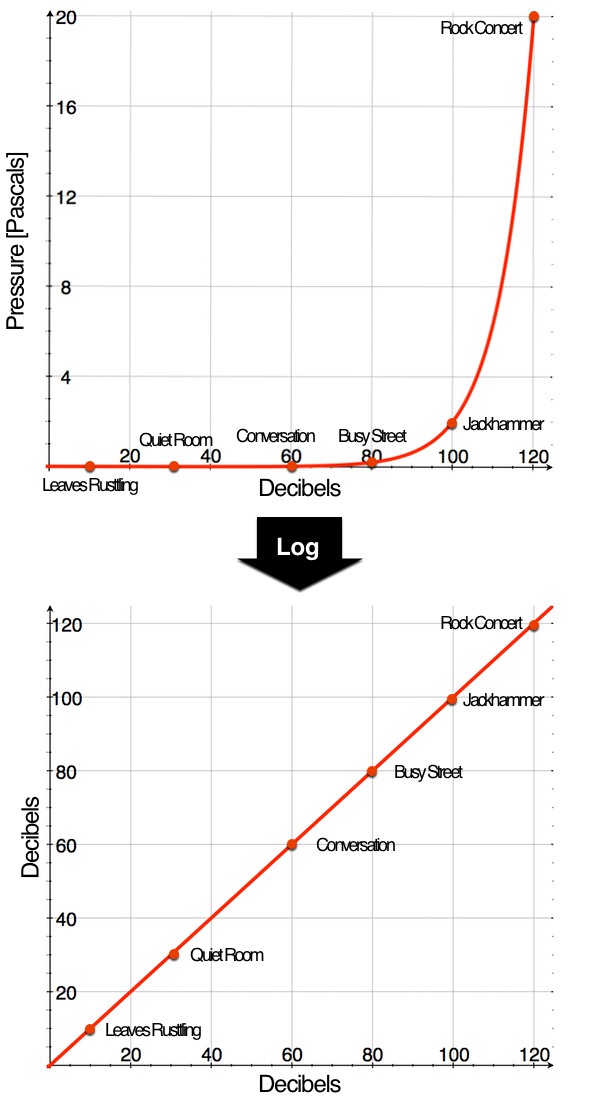
In a previous article we talked about the concept of scale, and how it relates to wavelength. We talked about how the wavelengths of sound cover a wide range of scales, and how it is the relative size of an object compared to that wavelength that determines its impact on sound. In many ways, the decibel is the unit that best handles data whose magnitude varies greatly. To find the decibel value for a given measurement, we must first take a ratio of that quantity with what is known as a “reference.” With all measures of scale, it is a matter of comparison, and the reference value is simply what we are comparing our current measurement to. After dividing by the reference, we take a logarithm, an operation which turns exponentially spaced values into linearly spaced ones. Because matters of scale tend to follow exponential rules, this operation makes these values much more manageable. Finally, we multiply the resulting value by either 10 or 20 (depending on what we are measuring) and we have expressed our initial value in decibels!
So, what value do we insert into the above equation to find decibels? While you can represent sounds in terms of energy or power, the most common measure is pressure, with the SI unit of Pascals (Pa). Sounds cover a wide range of pressures, with very loud sounds being hundreds of Pascals, and the quietest being measured in micro Pascals (µPa). And while this does cover a large range, even very loud sounds still have pressures well below atmospheric pressure, at around 101,000 Pa at sea level.
For a simple example of calculating decibels, consider a quiet room with a normal background sound of 2 mPa. We divide by 20 µPa (the reference pressure used for sound), giving us 100. We take the base 10 logarithm (which translates the number to a power of ten), which gives us 2. Then we multiply by 20, giving us a final value of 40 dB! If, instead, we had a very loud room at 200 mPa, and go through the same process, we get a value of 80 dB! And the sound of a concert at 20 Pa would be 120 dB.
The logarithm function makes decibel values much more manageable than simple pressures, by making exponential relationships into linear ones. (click to enlarge image)
There are several practical reasons why decibels are so widely used in acoustics. For one, acoustic pressures cover a very wide range of scales, with the sound pressure produced by leaves rustling in a forest being one trillionth of the pressure produced by a jet engine. Decibels are very good at representing those differences of magnitude. Without use of the decibel, the scale on which we’d have to put these sounds would be so large as to make representation very hard. Additionally, when sound spreads from a source it often follows what is sometimes called the “Inverse Square Law” which says that the pressure falls off at a rate proportional to the square of the distance to the source. When converted to decibels, this translates to a linear loss of 6 dB every doubling of distance.
However, there is one more reason why decibels have become so popular: they approximate how humans perceive sounds. Human hearing roughly follows what is known as the Weber-Fechner Law, which states that both the just-noticeable difference between two stimuli and the subjective perception of stimuli is proportional to the magnitude of the stimuli. In relation to sounds, this means that the louder the sound, the more of an increase is needed to be noticed, and the perception of a sound’s loudness is essentially related to scale. In other words, an increase from 2 to 20 Pa (a change of 18 Pa), would be perceived the same as an increase from 20 to 200 Pa (a change of 180 Pa!) because both are changing by a factor of 10.
The Weber-Fechner law is very reminiscent of the decibel. The reference value sets the point of comparison for the just-noticeable difference, and the logarithm makes changes in magnitude linear. The traditional reference value used for sound in air even reflects this, because it was selected to be the quietest sound that a young person with healthy hearing can detect at 1000 Hz (20 µPa), setting the baseline of 0 dB. Based on the Weber-Fechner law, acousticians have developed a simple rule of thumb: every 10 dB is perceived as a doubling of loudness. While this is not perfect, it is close-enough to be useful.
And this brings us to the concept of a metric. While the term metric has many uses throughout many disciplines, at its core it just means a single number used to describe something. The distance between two points is a metric used to describe their relative positions, for example. Many values are difficult, if not impossible, to measure directly. For acoustics, the question often is “how loud does this sound seem?” Without getting inside a person’s head, this is hard to measure. You might ask people to answer a questionnaire, but that is not very reliable and is ultimately very difficult to design around. Instead, we rely on the Weber-Fechner law and use the decibel as the de facto metric for loudness.
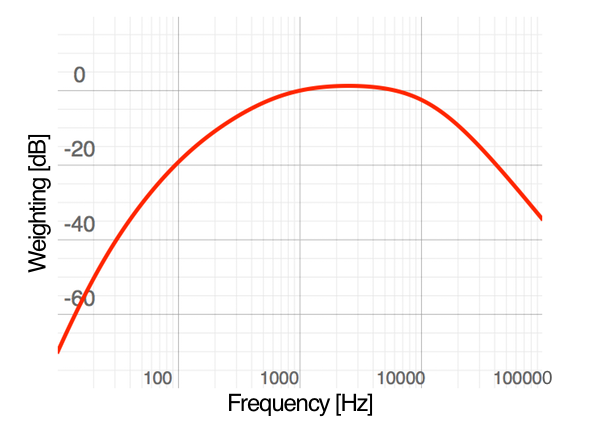
Of course, there are some limitations to this. As mentioned in the article on frequency, there are sounds outside of the human hearing range that a person cannot normally detect, and others which are more or less noticeable. Yet, using a sensitive enough microphone, all of those sounds might still contribute equally to a basic measure of the sound level. To alleviate this, the sound measurement is taken with a frequency weighting to better approximate human hearing. The most common of these, by far, is known as the A-weighting, which approximates the human hearing system when exposed to the quietest of sounds.
The A-weighting approximates human hearing by reducing the contributions of both low frequency and high frequency sounds. (click to enlarge image)
With all of this in mind, the values of A-weighted sound levels are actually quite intuitive. A level of 0 dB would be the quietest sound that a young person with healthy hearing could detect, and a level of 100 dB would usually be considered very loud. In between you have the sound of a quiet home, often sitting around 40 dB, or the sound of a bustling city street which might get up to 80 dB. And while you could just guess what the sound level of a given sound is, technology has advanced to the point where an inexpensive smartphone app can now rival the purpose-built sound level meters that acousticians use.
There is certainly more that can be said about decibels, including alternative frequency weighting schemes and the differences between decibel values measured in air and water, but for now I would like to leave you with those simple rules of thumb that will allow even a non-scientist to interpret an acoustic decibel level with ease. If the sound level measurement is made in air with the standard reference values and the most common weighting, then a value of 0 dB is on the threshold of silence, 40 dB would be quiet, 80 dB would be loud, and 120 dB would border on unbearable, and every 10 dB increase “doubles” the perceived volume. With these landmarks and that simple rule of thumb, the decibel will not be such a mystifying value!
Next time on the world through sound we will consider acoustic mediums, and discuss the importance of not just the sound, but the material that sound moves through.