11 • The World Through Sound: Linearity

Welcome to another installment of The World Through Sound. Last time, we talked about reflection and refraction, and the principle of least time that governs them. This week we will discuss linearity, superposition, and how science uses approximations to make the messiness of reality a bit more manageable.

Linearity is one of the most useful features that a system can have, and there’s an entire branch of mathematics devoted to linear systems theory. With that in mind, what makes a system linear? Simply put, a system is considered linear if the equations that govern it follow the simple rule that the sum of the inputs to the system yields the sum of the outputs. Put mathematically, if H( ) describes my system, and x and y are my inputs, then H(x+y) = H(x) + H(y). And while this may seem rather trivial, the effects of this property are quite profound.

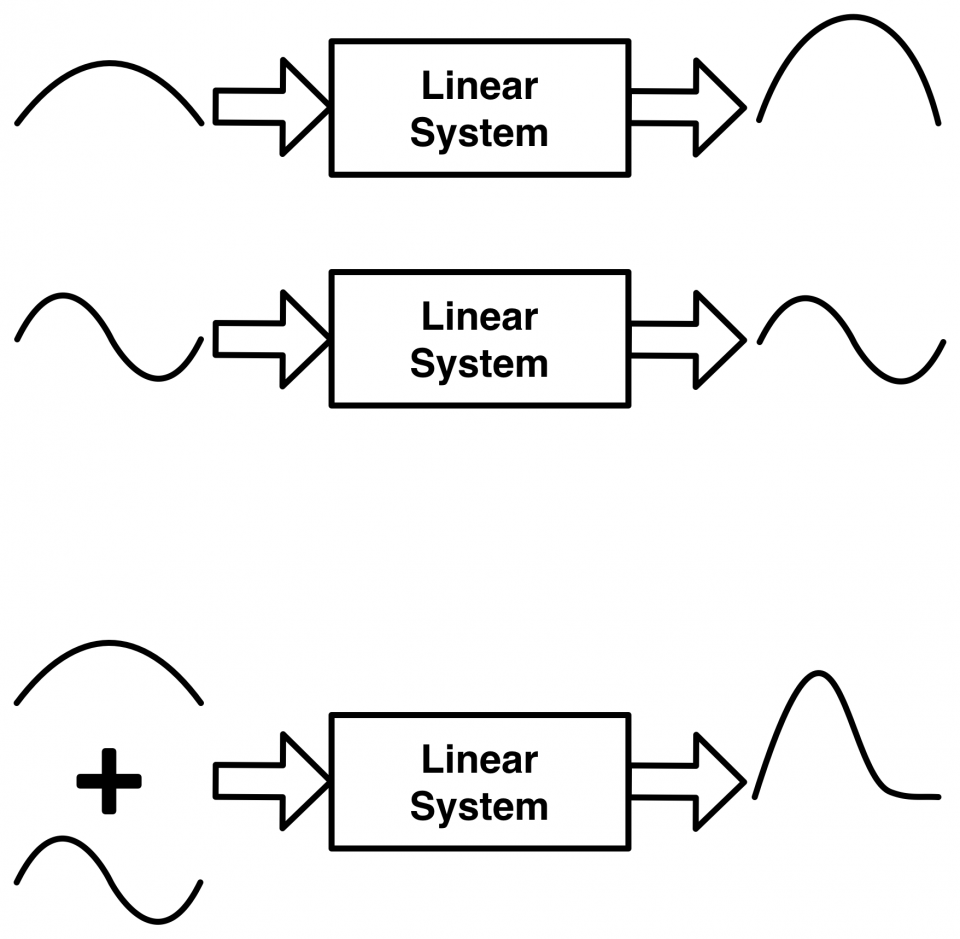
Linear systems make things really simple, and who doesn’t like when things are simple?

The biggest benefit of linearity is that it allows us to use the tool of superposition. Superposition says that if I know two separate solutions to a system, then I know that the sum of those solutions is also a solution to the system. The system could be very complex, it could even be a completely unknown black box, but as long as I know that the system is linear, I can use superposition to predict what I’ll get out of it.

Acoustics is absolutely rife with linearity. Nearly every acoustic system is linear to a high degree. For most sounds that you hear, air is a linear medium. That is, the sound pressure in the air is simply the sound pressures from every source contributing sound added together. The ocean is also a linear medium for sound. Speakers respond linearly to the voltage going into them (good ones do, at least), and the natural vibrations of most objects and resonators are also linear.

Ever wonder how to generate these interesting looking interference patterns? Thanks to linearity and superposition, the answer is as simple as 1+1.

Because all of these systems are linear, scientists make regular use of superposition. The reason why normal modes are so fundamental is that the modes, which are just solutions to the equations of motion of the system, can be added together to find all new solutions. Acoustic impedance can give a full description of the behavior of a linear system, using superposition. We regularly take complicated problems with lots of sound sources at different levels in different locations, and make the problems easier by breaking them up and solving them piece by piece. Because of superposition, scientists can find an answer, and keep using that same answer over and over again without having to worry that it’s changed.

Unfortunately, not everything is linear, and sometimes superposition doesn’t work. This is called non-linearity, and it also has its place in acoustics. You may have heard of a shock wave. These powerful waves often occur with an explosion, and are also generated when something breaks the speed of sound (a so-called “Sonic Boom.”) Shock waves are acoustic waves, but they certainly aren’t linear. For example, the more powerful the shock wave is, the faster it moves. So if I took two identical shock waves, and added them together, the resulting shockwave would move faster than either of those shock waves alone. This is because sound speed is a function of pressure, so as acoustic pressure increases, so does the speed of the wave.

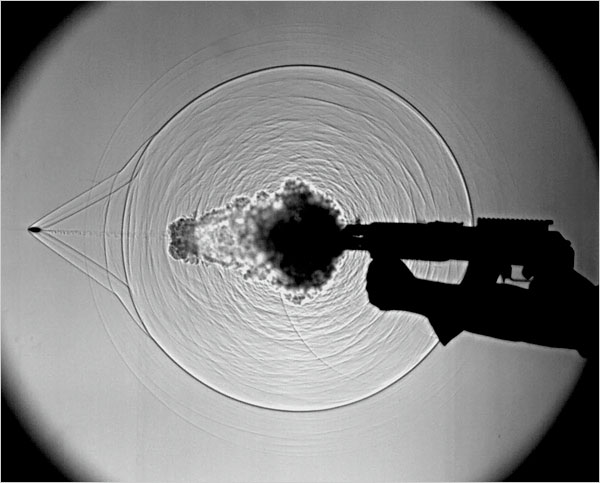
“Not all waves are linear. The shockwaves from an explosion or supersonic object are so extreme that they behave differently than less intense sounds.” Photo credit Gary Settles/Penn State

If you read that last sentence carefully, you might notice something fishy. Don’t all sound waves cause a change in acoustic pressure? And if that’s true, then shouldn’t all sound waves change the speed of sound, and thus act non-linearly? And while that may be true, that brings us to the concept of approximation, linearization, and how science often bends (or rather straightens) the truth to make things simpler, giving us more elegant and useful solutions.

Approximation is one of science’s favorite tools. Real systems are often complicated, often messy, and depend on an extremely large number of factors. But many of these factors are very minor, and can be reasonably ignored in most circumstances. But even if you can narrow a problem down to a single important factor, the relationship between the input and output of a system over the entire range of inputs often looks quite strange, and doesn’t hold to linearity. But thanks to calculus, we know that no matter how complicated a function looks, if we zoom in close enough that function starts to look like a line. Zooming in like this is called a “First Order Approximation,” so-named because the solution is found by using only the first order term of the Taylor series expansion of the full solution. With this, we can turn any continuous function, be it a parabola, hyperbola, or even a sine wave, into a line. This process is called “linearization,” and it’s used to treat a nonlinear system like a linear system within certain limits. Generally, this linearization will break down when your input strays too far from the point it’s linearized around, but within that range we can apply superposition and all of the other linear system analysis tools that are so powerful.

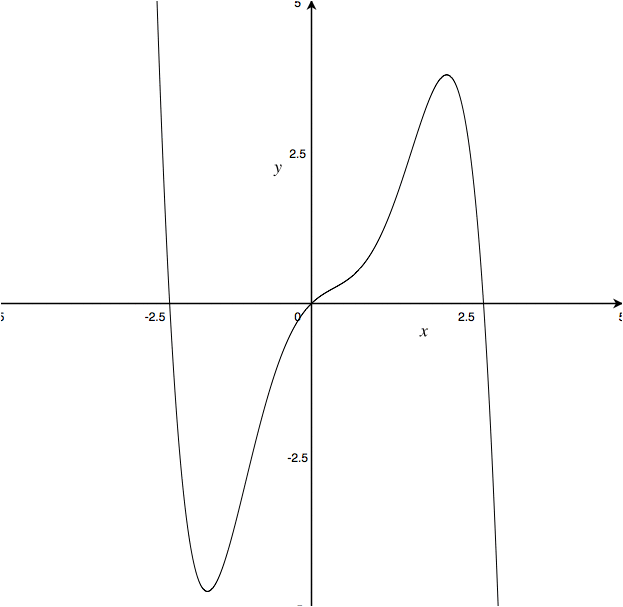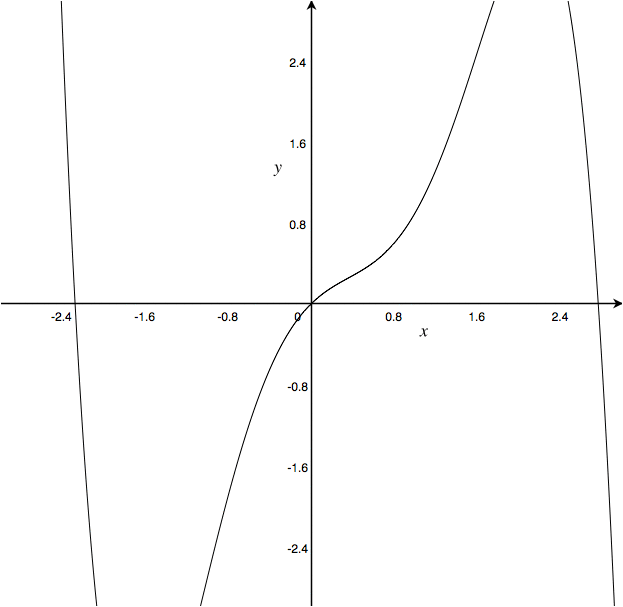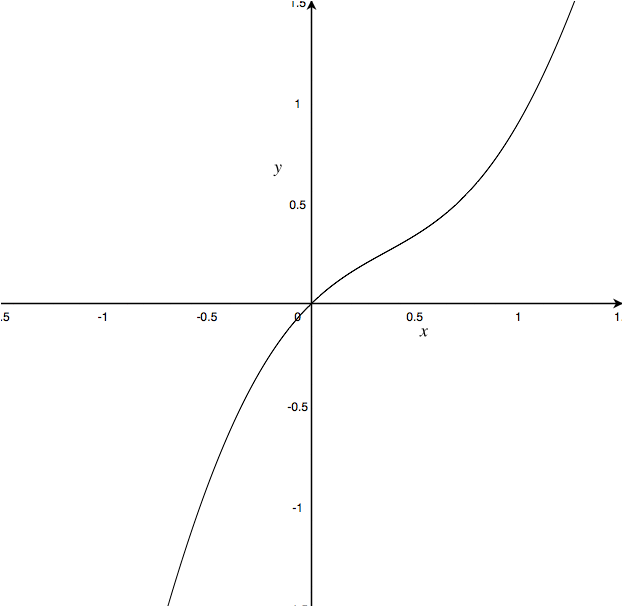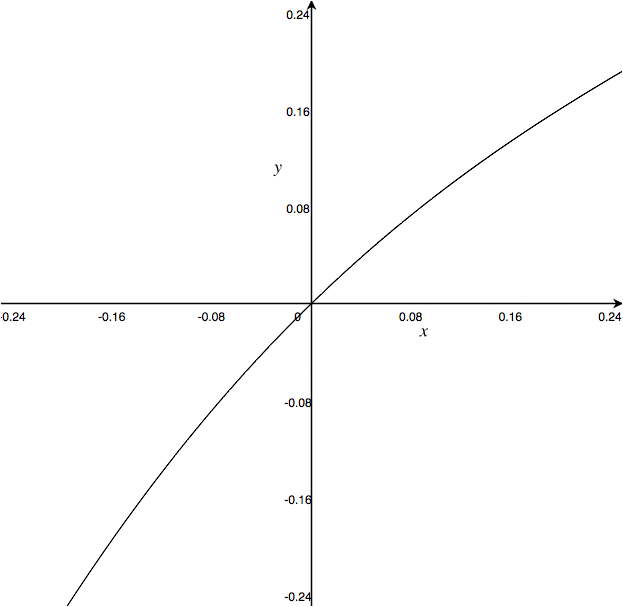
No matter how complicated a function is, on some level it’s linear.

But if we know the true equations governing the system, even without this linearization, why do scientists even bother? The primary answer is insight. Science’s purpose is not just to get the right answer, but also to help us understand the natural world. And part of understanding is knowing what things are important, and what things aren’t. Through approximations, we can simplify a problem by throwing out everything that’s unimportant, and when linearization gets too far from the real answer, we can start to add those complications back in.

Next time, in our final installment of The World Through Sound, we will talk about acoustic absorption, and how sound is more than just pressure.

Next Article…